La suite de Syracuse
Enoncé de la conjecture - Idées de programmation - Calculer les termes de la suite de Syracuse en ligne - Records
Commentaires sur la conjecture de Collatz
Le problème 3x+1 ou la conjecture de Syracuse ou de Collatz (nom du mathématicien qui l'a le plus répandu) est d'une étonnante simplicité, mais elle résiste pourtant au effort des mathématiciens à la démontrer (ou pas) depuis le milieu du 20 siècle. C'est pour cela que son énoncé reste une conjecture.
Cette conjecture est apparue vers 1930 et s'est répandue vers 1950 grâce notamment à l'université de Syracuse, d'où le nom. Le nom, mais aussi les noms qui sont nombreux : conjecture de Collatz, conjecture de Syracuse ou problème de 3x+1. Un problème qui reste entièrement ouvert encore aujourd'hui.
La suite de syracuse de Collatz ( Lothar Collatz )
On choisit un nombre entier :
- Si le nombre est pair, on le divise par 2 et on obtient le terme suivant de la suite.
- Si le nombre est impair, on le multiplie par 3, on ajoute 1 au résultat et on obtient le terme suivant de la suite.
On recommence la procédure avec le nouveau nombre obtenu.
On obtient une suite de nombres qui est appelée :
- le vol du nombre de départ,
- les nombres de la suite sont appelés les étapes du vol,
- le plus grand nombre obtenu dans la suite est appelé l'altitude maximale du vol,
- le nombre d'étapes avant de passer sous le nombre de départ est appelé la durée du vol en altitude,
- le nombre d'étapes avant d'obtenir 1 est appelé la durée du vol.
Une fois atteint le nombre 1, la suite des valeurs (1,4,2,1,4,2…) se répète indéfiniment en un cycle de longueur 3, appelé cycle trivial.
Nous pouvons définir la suite sous la forme qui suit, pour tout entier n > 1 :
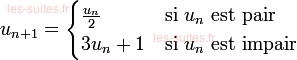
Conjecture de Syracuse Collatz :
Quel que soit le nombre de départ dans la suite obtenue avec l'algorithme de Syracuse de Collatz, on finit toujours par obtenir 1.
Mais, pour le moment, cela reste une conjecture et aucune preuve (démonstration) n'a été établie à ce jour.
Les avancées
(ce qui est démontré à ce jour nov 2011)
La conjecture de Syracuse est équivalente à l’un des énoncés suivants :
(1) la durée de tout vol est finie ;
(2) la durée de tout vol en altitude est finie ;
(3) tout vol a un nombre fini d’étapes paires ;
(4) tout vol a un nombre fini d’étapes paires en altitude ;
(5) tout vol a un nombre fini d’étapes impaires ;
(6) tout vol a un nombre fini d’étapes impaires en altitude .
Les termes de la suite de syracuse pour 11,27,97,99
pour 11 nous obtenons :
2 - 1
La durée du vol pour 2 est de 1 et son altitude est de 2
3 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 3 est de 7 et son altitude est de 16
4 - 2 - 1
La durée du vol pour 4 est de 2 et son altitude est de 4
5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 5 est de 5 et son altitude est de 16
6 - 3 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 6 est de 8 et son altitude est de 16
7 - 22 - 11 - 34 - 17 - 52 - 26 - 13 - 40 - 20 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 7 est de 16 et son altitude est de 52
8 - 4 - 2 - 1
La durée du vol pour 8 est de 3 et son altitude est de 8
9 - 28 - 14 - 7 - 22 - 11 - 34 - 17 - 52 - 26 - 13 - 40 - 20 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 9 est de 19 et son altitude est de 52
10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 10 est de 6 et son altitude est de 16
pour 27 nous obtenons :
27 - 82 - 41 - 124 - 62 - 31 - 94 - 47 - 142 - 71 - 214 - 107 - 322 - 161 - 484 - 242 - 121 - 364 - 182 - 91 - 274 - 137 - 412 - 206 - 103 - 310 - 155 - 466 - 233 - 700 - 350 - 175 - 526 - 263 - 790 - 395 - 1186 - 593 - 1780 - 890 - 445 - 1336 - 668 - 334 - 167 - 502 - 251 - 754 - 377 - 1132 - 566 - 283 - 850 - 425 - 1276 - 638 - 319 - 958 - 479 - 1438 - 719 - 2158 - 1079 - 3238 - 1619 - 4858 - 2429 - 7288 - 3644 - 1822 - 911 - 2734 - 1367 - 4102 - 2051 - 6154 - 3077 - 9232 - 4616 - 2308 - 1154 - 577 - 1732 - 866 - 433 - 1300 - 650 - 325 - 976 - 488 - 244 - 122 - 61 - 184 - 92 - 46 - 23 - 70 - 35 - 106 - 53 - 160 - 80 - 40 - 20 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 27 est de 111 et son altitude est de 9232
pour 97 nous obtenons :
97 - 292 - 146 - 73 - 220 - 110 - 55 - 166 - 83 - 250 - 125 - 376 - 188 - 94 - 47 - 142 - 71 - 214 - 107 - 322 - 161 - 484 - 242 - 121 - 364 - 182 - 91 - 274 - 137 - 412 - 206 - 103 - 310 - 155 - 466 - 233 - 700 - 350 - 175 - 526 - 263 - 790 - 395 - 1186 - 593 - 1780 - 890 - 445 - 1336 - 668 - 334 - 167 - 502 - 251 - 754 - 377 - 1132 - 566 - 283 - 850 - 425 - 1276 - 638 - 319 - 958 - 479 - 1438 - 719 - 2158 - 1079 - 3238 - 1619 - 4858 - 2429 - 7288 - 3644 - 1822 - 911 - 2734 - 1367 - 4102 - 2051 - 6154 - 3077 - 9232 - 4616 - 2308 - 1154 - 577 - 1732 - 866 - 433 - 1300 - 650 - 325 - 976 - 488 - 244 - 122 - 61 - 184 - 92 - 46 - 23 - 70 - 35 - 106 - 53 - 160 - 80 - 40 - 20 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 97 est de 118 et son altitude est de 9232
C'est la même altitude maximale que pour 27 !
Nous pouvons remarquer que pour 99 nous obtenons une durée de vol beaucoup plus courte que pour 97 :
99 - 298 - 149 - 448 - 224 - 112 - 56 - 28 - 14 - 7 - 22 - 11 - 34 - 17 - 52 - 26 - 13 - 40 - 20 - 10 - 5 - 16 - 8 - 4 - 2 - 1
La durée du vol pour 99 est de 25 et son altitude est de 448
La suite de syracuse nous donne des résultats étonnants, qui sont impossibles à prévoir ! Essayez de trouver le plus long vol ou la plus haute altitude. Pour ma part je trouve 703 ou 871 intéressants.
Calculer le vol, la durée et l'altitude maximale d'un nombre
à vous de jouer... On ouvre un concours à celui qui trouvera la plus longue durée de vol ?
Vous pouvez par exemple tester (par ex ici : test syracuse) les nombres 703 et 871 qui sont, pour une valeur inferieure à 1000, les plus intéressants, l'un détient le record d'altitude et le second le record de durée, pour tous les nombres inferieurs à 1000.
Programmation Algorithme de Syracuse
Après avoir rédiger cette page, j’ai eu envie de voir ce que l'on pouvait faire en programmation, pour un simple mortel, c'est à dire :
- sans accès à du temps sur un très gros calculateur
- et sans avoir de bagage théorique permettant d’apprécier les dernières publications.
Mais c’est l’avantage de la conjecture, nous pouvons nous amuser et réussir quelques calculs sans travailler au Cnrs.
Les conditions étaient pour moi très réduites : un ordinateur portable, pas de logiciel qui me permettrait de compiler du C, j'étais donc réduit à monter un serveur web et de lancer une page web avec un programme de calcul rédiger en PHP. Le plus rapide et le simple, à mettre en œuvre, pour pouvoir tester des idées d'algorithmes.
Bref ! En reprenant les infos que l’on peut trouver sur la toile (enfin celle que les chercheurs veulent bien nous laisser) et en combinant cela avec les conditions particulières énoncées précédemment, voilà ce que j’ai pu obtenir en quelques jours de programmation et quelques heures de calcul.
Records d'altitude
n° - terme - durée en alt - alt max 1 - 27 - 96 - 9232 2 - 447 - 65 - 39364 3 - 639 - 37 - 41524 4 - 703 - 132 - 250504 5 - 1819 - 99 - 1 276936 6 - 4255 - 114 - 6 810136 7 - 4591 - 106 - 8 153620 8 - 9663 - 88 - 27 114424 9 - 20895 - 117 - 50 143264 10 - 26623 - 106 - 106 358020 11 - 31911 - 96 - 121 012864 12 - 60975 - 207 - 593 279152 13 - 77671 - 171 - 1570 824736 14 - 113383 - 179 - 2482 111348 15 - 138367 - 96 - 2798 323360 16 - 159487 - 117 - 17202 377752 17 - 270271 - 267 - 24648 077896 18 - 665215 - 228 - 52483 285312 19 - 704511 - 119 - 56991 483520 20 - 1042431 - 277 - 90239 155648 21 - 1212415 - 171 - 139646 736808 22 - 1441407 - 243 - 151629 574372 23 - 1875711 - 158 - 155904 349696 24 - 1988859 - 220 - 156914 378224 25 - 2643183 - 298 - 190459 818484 26 - 2684647 - 161 - 352617 812944 27 - 3041127 - 161 - 622717 901620 28 - 3873535 - 202 - 858555 169576 29 - 4637979 - 254 - 1 318802 294932 30 - 5656191 - 326 - 2 412493 616608 31 - 6416623 - 228 - 4 799996 945368 32 - 6631675 - 362 - 60 342610 919632 33 - 19638399 - 430 - 306 296925 203752 34 - 38595583 - 295 - 474 637698 851092 35 - 80049391 - 396 - 2185 143829 170100 36 - 120080895 - 331 - 3277 901576 118580 37 - 210964383 - 388 - 6404 797161 121264 38 - 319804831 - 427 - 1 414236 446719 942480
Récords de durée en altitude
| nombre | durée en altitude | durée | altitude |
|---|---|---|---|
| 703 | 132 | 170 | 250 504 |
| 10 087 | 171 | 223 | 2 484 916 |
| 35 655 | 220 | 323 | 41 163 712 |
| 626 331 | 287 | 508 | 7 222 283 188 |
| 1 126 015 | 365 | 527 | 90 239 155 648 |
| 8 088 063 | 401 | 566 | 16 155 154 672 |
| 63 728 127 | 613 | 949 | 966 616 035 460 |
| 217 740 015 | 644 | 793 | 2 516 021 527 120 |
| 2 788 008 987 | 729 | 944 | 81 887 769 175 732 |
| 1 200 991 791 | 649 | 873 | 35 681 506 677 556 |
| 1 827 397 567 | 706 | 928 | 118 736 698 851769012 |
| 2 788 008 987 | 729 | 944 | 81 887 769175732 |
| 12 235 060 455 | 892 | 1184 | 1 037 298 361093936 |
J'ai découvert que l'on pouvait compiler du C sur mon macbook ! Hé oui c'est livré avec le portable ! J'ai donc recompilé le tout en C, en améliorant l’algorithme, cette fois-ci tout va beaucoup plus vite, j'ai pu obtenir les records de vol en altitude ci-dessous en quelques centaines de secondes ! Ensuite, la suite de Syracuse avec comme premier terme 12 235 060455, le record suivant semble beaucoup mois abordable pour mon algorithme et ma machine, après une heure de calculs, j’obtiens un résultat surement faux car l’altitude dépasse les capacité des integer long long en C :/ Dommage ! J’ai bien tenté de créer une structure pour gérer les très grands entiers mais cela ralentit considérablement les calculs.
Record de durée en altitude avec le programme en C
27 - 96 - 9232 - 0.000005 s
703 - 132 - 250504 - 0.000107 s
10087 - 171 - 2484916 - 0.000183 s
35655 - 220 - 41163712 - 0.000361 s
270271 - 267 - 24648077896 - 0.001860 s
362343 - 269 - 565335124 - 0.002447 s
381727 - 282 - 565335124 - 0.002578 s
626331 - 287 - 7222283188 - 0.004115 s
1027431 - 298 - 17808240724 - 0.006625 s
1126015 - 365 - 90239155648 - 0.007248 s
8088063 - 401 - 16155154672 - 0.051004 s
13421671 - 468 - 1591706254336 - 0.084490 s
20638335 - 476 - 89243211616 - 0.129836 s
26716671 - 486 - 3696858621088 - 0.167983 s
56924955 - 502 - 7209046267252 - 0.357630 s
63728127 - 613 - 966616035460 - 0.400345 s
217740015 - 644 - 2516021527120 - 1.366941 s
1200991791 - 649 - 35681506677556 - 7.537392 s
1827397567 - 706 - 118736698851769012 - 11.468214 s
2788008987 - 729 - 81887769175732 - 17.496869 s
12235060455 - 892 - 1037298361093936 - 76.827696 s