accueil / sommaire cours terminale S / suites majorées, minorées et bornées

V Suites majorées, minorées et bornées

Soit (u_n)_n≥a une suite à termes réels, elle est majorée (respectivement minorée) s'il existe une constante M (respectivement m) telque pour tout entier n ≥ a on a u_n ≤ M (respectivement u_n ≥ m).

M est alors un mojorant de la suite et m est alors un minorant de la suite.

La suite est bornée si majorée et minorée alors il existe une constante μ ≥ 0 telque pour tout entier n ≥ a,

∣ u_n∣ ≥ μ.

1) Comparaison directe de u_n à M ou à m

exemple :

Soit U = (u_n)_n≥0 telque pour tout n ≥ 0 on a u_n = (2n + 1)÷(n + 1)

Montrer que la suite U est majorée par 2.

Pour tout entier n ≥ 0 u_n − 2 = − 1 ÷ (n + 1) < 0

Conclusion : pour tout entier n ≥ 0 u_n < 2 CQFD.

2) Suite donnée de manière explicite

Par u_n = ƒ(n), ƒ étant une fonction numérique définie sur [a; +∞[. L'etude des variation de ƒ sur son domaine permet évantuellement de trouver un majorant ou un minorant de ƒ sur [a; +∞[ donc de la suite.

exemple :

Soit U = (u_n)_n≥0 telque pour tout n ≥ 0 on a u_n = (3n − 5)÷(2n + 1)

et la fonction ƒ : ℜ → ℜ x →ƒ(x) = 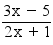on a Dƒ = ℜ\{−1/2}.

Pour tout entier n ≥ 0 u_n = ƒ(n) on a [0;+∞[ ⊂ Dƒ.

Pour tout x ∈ Dƒ, ƒ'(x) =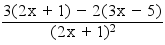= 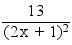> 0

donc ƒ est strictement croissante sur [0;+∞[ .

On a ƒ(0) = − 5 et lim_x→+∞ƒ(x) = 3/2 donc ∀ x ∈ ℕ ƒ(x) ∈ [− 5;3/2] .

Conclusion : la suite U est bornée, elle est majorée par 3/2 et minorée par − 5.

3) Cas des suites récurrentes

exemple :

Soit U = (u_n)_n≥0 définie par :

u₀ = λ = constante ∈ [0;1/2] et ∀ n ∈ ℕ, u_n+1 = u_n² + u_n ÷ 2 = .

Montrons que ∀ n ∈ ℕ, u_n ∈ [0;1/2].

Par récurrence :

Soit P(n) l'énoncé " u_n ∈ [0;1/2] ".

P(0) est vrai.

Soit n un entier ≥ 0 quelconque telque P(n) soit vrai, c'est-à-dire que 0 ≤ u_n ≤ 1/2 (hypothèse de récurrence).

Montrons que P(n+1) est vrai c'est à dire c'est-à-dire que 0 ≤ u_n+1 ≤ 1/2 .

démonstration :

Nous avons 0 ≤ u_n ≤ 1/2

d'où 0 ≤ u_n² ≤ 1/4 et aussi 0 ≤ u_n ÷ 2 ≤ 1/4

d'où

0 ≤ u_n² + u_n ÷ 2 ≤ 1/4 + 1/4

0 ≤ u_n² + u_n ÷ 2 ≤ 1/2

0 ≤ u_n+1 ≤ 1/2

donc P(n+1) est vrai.

conclusion : P(0) est vrai et P(n+1) Iest vrai donc l'enoncé de récurrence est vrai et nous avons montré que u_n ∈ [0;1/2] pour tout n entier naturel positif.

Autre méthode :

La suite est récurrente, soit la fonction ƒ ℜ → ℜ : x →ƒ(x) = ²x + x/2, la suite est alors définie par :

u₀ = λ = constante ∈ [0;1/2] et ∀ n ∈ ℕ, u_n+1 =ƒ(u_n).

I = [0;1/2]

Pour tout n entier naturel u_n ∈ [0;1/2], il suffit de vérifier que :

u₀ ∈ I et ƒ(I) ⊂ I c'est-à-dire ∀ x ∈ I , ƒ(x) ∈ I.

En effet, nous avons u₀ ∈ [0;1/2] et pour tout n ≥ 0 telque u_n ∈ [0;1/2] alors u_n+1 = ƒ(u_n) ∈ ƒ([0;1/2])

d'où u_n+1 ∈ ƒ([0;1/2]) .

Pour établir ƒ(I) ⊂ I, on étudie les variations de ƒ sur I. ƒ est continue dérivable sur I .

∀ x ∈ I , ƒ'(x) = 2x + 1/2 > 0 , donc ƒ est strictement croissante sur I donc ƒ(I) = [ƒ(0);ƒ(1/2)] = [0;1/2]

donc ƒ(I) ⊂ I CQFD .

Conclusion : on a bien ∀ n ∈ ℕ, 0 ≤ u_n ≤ 1/2 la suite est bornée.

4) Généralisation

Soit U = (u_n)_n≥a la suite à termes réels définie par son premier terme u_a et par la relation :

∀ n ≥ a u_n+1 = ƒ(u_n), ƒ étant une fonction numérique donnée.

Si nous voulons montrer que pour n entier ≥ a , u_n ∈ I. I étant un intervalle donné inclus dans le domaine de définition.

Nous pouvons utiliser la méthode suivante :

i) vérifier que u_a ∈ I

ii) vérifier si ƒ(I) ⊂ I par exemple en étudiant les varations de ƒ sur I ou en grâce à une récurrence.