accueil / sommaire cours terminale S / égalité de suites

IV Egalité de suites

Soient (u_n)_n≥a et (v_n)_n≥a,, 2 suites à termes réels ou complexes de même ensemble d'indices, elles sont égales si pour tout entier > a nous avons u_n = v_n.

1) Cas d'une suite récurrente

Soit U = (u_n)_n≥a une suite récurrente définie de façon unique par la donnée de son premier terme u₀ et pour tout entier n ≥ a par la relation suivante u_n+1 = φ(u_n) , φ étant une fonction numérique donnée.

Soit V = (v_n)_n≥a une seconde suite , pour montrer que u_n = v_n,

il suffit de montrer que : u_a = v_a et pour tout entier n ≥ a v_n+1 = φ(v_n) .

2) Exercice

Soit U = (u_n)_n≥a une suite à termes réels définie par : u₀ = 1 et ∀ n ∈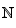 u_n+1 = u_n ÷ (1 + u_n)

Montrer que pour tout n entier naturel nous avons u_n = 1 ÷ (1 + n) .

Soit la fonction ƒ : ℜ → ℜ, x → ƒ(x) = , la suite U est définie par : u₀ = 1 et ∀ n ∈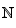 u_n+1 = ƒ(u_n).

On pose v_n = 1 ÷ (1 + n) pour tout n ∈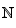 on veut montrer que u_n = v_n.

On a v₀ = 1 ÷ (1 + 0) = 1 = u₀ (i)

∀ n ∈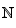, v_n+1 = 1 ÷ (1 + n+1) = 1 ÷ (2 + n)

∀ n ∈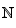, ƒ(v_n) = v_n÷ (1 + v_n) = = = = 1 ÷ (2 + n) = v_n+1

On a ∀ n ∈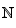, v_n+1 = ƒ(v_n) (ii)

De (i) et de (ii) nous pouvons conclure que la suite U est égale à la suite V

et donc que ∀ n ∈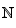, u_n = 1 ÷ (1 + n) CQFD.