accueil / sommaire cours terminale S / détermination d'une suite à terme réels ou complexes

III Détermination d'une suite à terme réels (respectivement complexes)

1) Suite définie par une formule explicite

Soit a entier naturel donné et ƒ une fonction de variable réelle à valeur dans ℜ ( respectivement dans 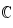) telque le domaine de définition contienne tous les entiers ≥ a, nous pourrons définir une suite (u_n)_n≥a par la relation suivante : pour tout entier n ≥ a, u_n = ƒ(n).

exemple 1 :

suite à termes réels (u_n)_n≥0 avec u_n = sin(n²)÷(n+3).

Soit ƒ la fonction numériques de variable réelle x définie sur ℜ\{3} par ƒ(x) = sin(x²)÷(x+3).

ƒ est bien définie pour tout x ∈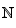et nous avons, ∀ x ∈ 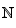u_n = ƒ(n).

2) Suite définie par une relation de récurrence

Une suite (u_n)_n≥a à termes réels (respectivement complexe) est déterminer de manière unique lorsque l'on se donne son premier terme u_n = λ , λ étant un réel (respectivement complexe) donné et la relation de récurrence pour tout entier ≥ a, u_n+1 = φ(n). φ étant une fonction de ℜ dans ℜ (respectivement de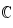dans).

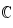exemple :

Soit U la suite numérique (u_n)_n≥0 définie par : u₀ = 1 et ∀ n ∈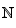 u_n+1 = u_n÷3 + 2 .

Soit la fonction φ : ℜ → ℜ, x →φ(x) = et ∀ n ∈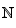 u_n+1 = φ(n).

u₀ = 1

u₁ = φ(u₀) = φ(1) = 1/3 + 2 = 7/3

u₂ = φ(u₁) = φ(7/3) = 7/9 + 2 = 25/9

u₃ = φ(u₂) = φ(25/9) = 25/27 + 2 = 79/27

u₄ = φ(u₃) = φ(79/27) = 79/81 + 2 = 241/81

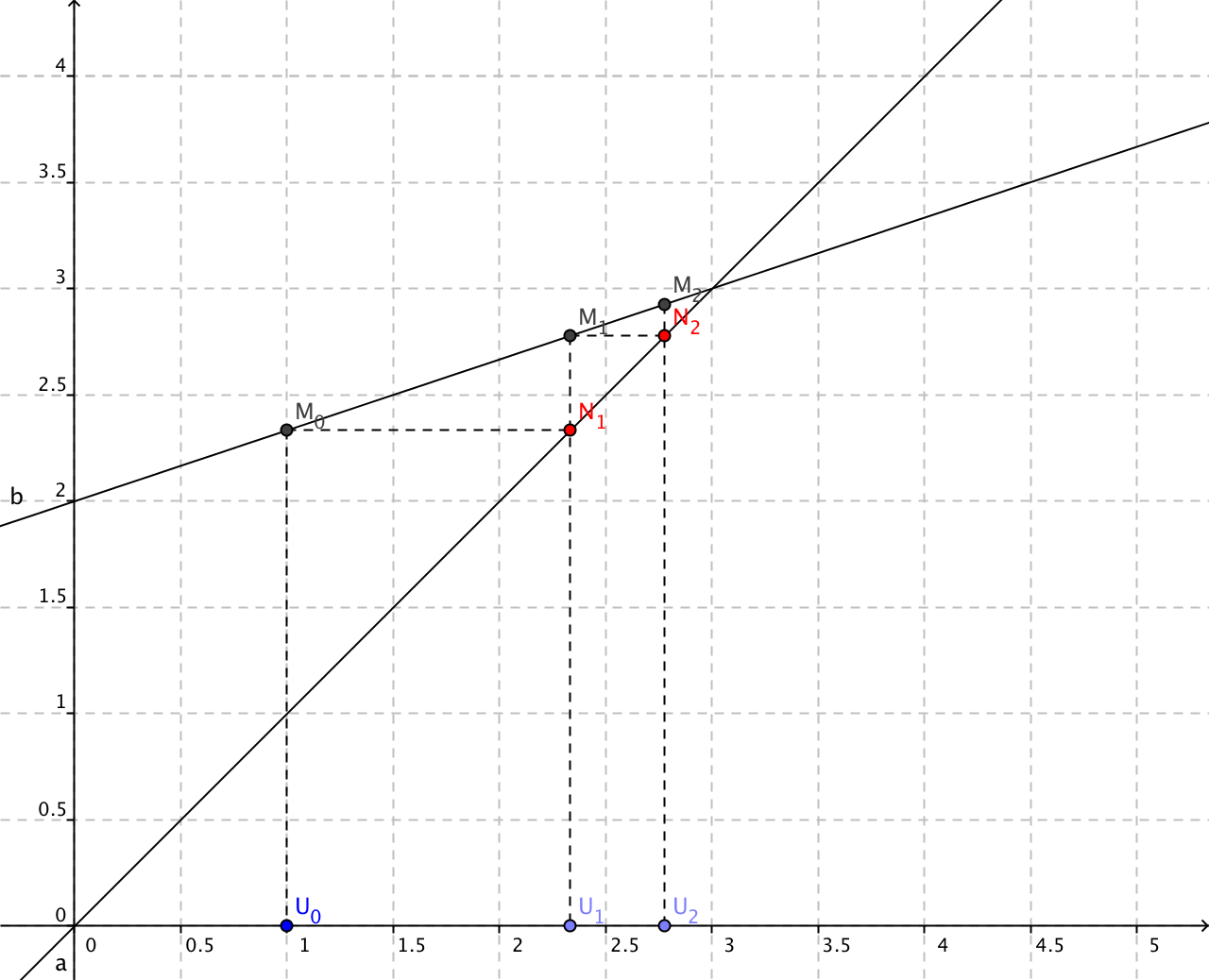
Ici la droite d'équation y = x/3 + 2 et la droite d'équation y = x se coupent en A(3;3).

Nous lisons les valeurs de u₀, u₁, u₂ sur l'axe des abscisses en procédant comme suit.

Marquer en abscisse le premier terme ici u₀ = 1 et u₁ = φ(u₀) est l'ordonnée du point M₀ d'abscisse u₀. Nous reportons cette ordonnée grace à la droite y = x. Soit N₁ le point d'ordonnée u₁ de la droite y = x, donc d'abscisse u₁ également.

u₂ = φ(u₁) est l'ordonnée du point M₁ d'abscisse u₁ et N₂ est le point d'ordonnée u₂ de la droite y = x, donc d'abscisse u₂ également.

La lecture du graphique permet de conjecturer que : u₀ < u₁ < u₂ < u₃ < 3, nous pouvons penser que la suite est strictement croissante et majorée par 3 et nous pouvons penser aussi que la lim_n→+∞u_n = 3 .