accueil / sommaire cours terminale S / définition d'une suite
II Définition d'une suite
1) Défintion
Une application U est appelées une suite si sa source est une partie, non vide, des entier naturels, c'est-à-dire si sa variable prend seulement comme valeurs "des entiers naturels".
Soit E un ensemble non vide quelconque et I une partie non vide de N.
Soit une application U de I vers E est une suite définie sur I à valeurs dans E. Pout tout entier naturel n élément de I on note U(n) : un "u indice n".
La suite est notée U = (un)n∈I, suite de terme générale de un indexée sur I.
Si I est fini, la suite est dite finie.
Si I est infini, la suite est dit infinie.
Si E est ℜ ou une partie de ℜ, la suite numérique est une suite à termes réels.
Si E est l'ensemble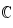 
ou une partie de 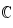, la suite numériques est une suite à termes complexes.
Dans la pratique, nous prendrons comme partie I de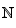 
l'ensemble des entiers supérieurs à un entier naturel a.
I = {n ∈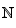/ n ≥ a} = {a, a+1, a+2, a+3, ...}
La suite est notée (un)n≥a alors :
- le premier terme de la suite est ua
- le deuxième terme de la suite est ua+1
- le troisième terme de la suite est ua+2
...
- le k ième terme de la suite est ua+k−1