accueil / sommaire cours première S / exercices sur les limites de suites
VI bis Exercices sur les limites des suites
Déterminer, si elle existe, la limite des suites suivantes :
1°) (un)n≥0 définie par la relation suivante : un = 5n7
on a limn→+∞ n7 = +∞ comme 5 est une constante > 0 on obtient limn→+∞ un = +∞
2°) (un)n≥0 définie par la relation suivante : un = −7 × 5n
5 est une constante > 1 alors limn→+∞ 5n = +∞ d'où limn→+∞ un = −∞
3°) (un)n≥0 définie par la relation suivante : un = 5n3 − 3n² − 5n − 7
Soit la fonction numérique ƒ : x →ƒ(x) = 5x3 − 3x² − 5x− 7 définie sur l'ensemble des réels tels que pour tout n > 0, un = ƒ(n)
or limx→+∞ ƒ(x) = +∞ donc limn→+∞ un = +∞
4°) (un)n≥6 définie par la relation suivante : un = [2n² + 3n − 5]/[5 − n]
Soit la fonction ƒ : x →ƒ(x) = [2x² + 3x − 5]/[5 − x] =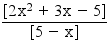 
définie sur ]−∞ ; +∞[ \ {5} tel que pour tout n ≥ 0, un = ƒ(n).
Déterminons la limite de la fonction pour trouver la limite de la suite.
Comme nous avons limx→+∞ ƒ(x) = −∞ alors limn→+∞ un = −∞.
5°) (un)n≥0 définie par la relation suivante : un = 3n² − 5n + 3sin(nπ/3) =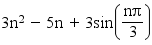 
On utilise la téchnique de majoration et minoration pour trouver la limite.
Pour tout n ∈
, −1 ≤ sin(nπ/3) ≤ 1 d'où −3 ≤ sin(nπ/3) ≤ 3 ou encore
et de là 3n² − 5n − 3 ≤ un ≤ 3n² − 5n + 3.
Or limn→+∞ 3n² − 5n − 3 = +∞ donc limn→+∞ un = +∞
6°) (un)n≥6 définie par la relation suivante : un = 37 − 2n − 3 × 11n
Première méthode pour trouver la limite de la suite : majorée et minorée la suite
On sait que : limn→+∞ (− 3 × 11n) = −∞ et pour tout n > 19, un ≤ 0 car 37 − 2n ≤ 0 donc limn→+∞ un = −∞
7°) (un)n≥0 définie par la relation suivante : un = 3√(n³ + 1) + 5 × 21n + 3 = 
On a limn→+∞ (n³ + 1) = +∞ de là limn→+∞ 3√(n³ + 1) = +∞
On a limn→+∞ (21n) = +∞ car 21 > 1, de là limn→+∞ (5 × 21n + 3) = +∞
d'où limn→+∞ un = +∞.