accueil / sommaire cours première S / convergence d'une suite vers 0
VII Convergence d'une suite vers zéro
Exemple : soit la suite U=(un)n>0 définie par la relation suivante : un = 1/n.
Pour avoir, la valeur absolue de la suite U, |un| < 1/10 , il suffit que n ≥ 10.
Pour avoir |un| < 10−4 , il suffit que n ≥ 10000.
Pour avoir |un| < 10−50 , il suffit que n ≥ 1050.
On arrive à rendre, la valeur absolue de un : |un| aussi proche que voulu de 0, dés que l'on prend l'entier naturel n suffisament grand.
On écrit limn→+∞ un = 0.
1°) Définition
Soit une suite numérique U=(un)n≥0, on dit qu'elle a pour limite 0, qu'elle converge vers 0 et on écrit limn→+∞ un = 0.
Si |un| peut être rendu aussi proche que voulu de 0 dés que l'entier n est pris suffisament grand :
limn→+∞ un ⇔ limn→+∞ |un|
2°) Exemples à connaitre
Soit a ∈ ℕ* les suites (1/n)n≥a , (1/n²)n≥a , (1/n³)n≥a , ... , sont convergentes vers 0.
Soit a ∈ ℕ* la suite (1/√n)n≥a converge vers 0.
Soit q une constante réelle ∈ ]-1;1[ , la suite (qn)n≥a converge vers 0.
3°) Théorèmes
a) Si la suite (un) converge vers 0 et la suite (vn) converge vers 0 alors :
limn→+∞ (un + vn) = 0 et limn→+∞ (un × vn) = 0.
b) soit un a un réel et soit ƒ une fonction numérique définie sur [a ; +∞[ , nous pouvons définir la suite U=(un)n≥0 telle que un = ƒ(n) si limn→+∞ ƒ(x) = 0 alors limn→+∞ un = 0.
c) Si 2 suites (un) et (vn) sont telles que il existe un entier p, tel que pour tout n ≥ p, on a |un| ≤ vn et la limn→+∞ vn = 0 alors : limn→+∞ un = 0
4°) Exercices sur la convergence vers 0
a) exercice 1
Soit une suite U=(un)n>0 telle que pour tout n ∈ ℕ*, un = sin(n)/n³ =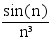 
. Montrons que cette suite est convergente vers 0.
∀ n ∈ ℕ*, |un| = |sin(n)|/n³ =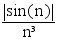 
d'où ∀ n ∈ ℕ* , |un| < 1/n³
comme la limite de (1/n³)est égale à 0 lorsque n tend vers +∞, donc on obtient limn→+∞ un = 0 d'après le théorème c)
b) exercice 2
Soit une suite U=(un)n≥0 telle que pour tout n ∈ ℕ, définie par la relation un = (−7/10)n / (n² + 1) =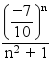
Montrons que cette suite converge vers 0.
Première méthode :
un = vn × wn avec vn = (−7/10)n et vn = 1/(n² + 1)
limn→+∞ vn = 0 car −7/10 est une constante ∈ ]−1;1[
limn→+∞ wn = 0 car limn→+∞ (n² + 1) = +∞
d'où limn→+∞ un = 0.
Dexième méthode : majorée |un|
|un| = (7/10)n / (n² + 1) =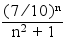 
pour tout n ∈ ℕ, n² + 1 ≥ 1 > 0 d'où 1/(n² + 1) ≤ 1
et de là pour tout n ∈ ℕ, |un| =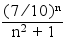 ≤ (7/10)n
Or on a limn→+∞ (7/10)n = 0 car 7/10 est une constante ∈ ]−1;1[ donc limn→+∞ un = 0 d'aprés le théorème c)
c) exercice 3
Soit une suite U=(un)n≥0 telle que pour tout n ∈ ℕ, définie par la relation un = (5n + 1) / (n² − 4 ) =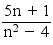 
Soit la fonction numérique ƒ : x → ƒ(x) = (5x + 1) / (x² − 4) =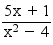
définie sur ]−∞;2[ ∪ ]2;+∞[, donc sur ]3;+∞[ tel que un = ƒ(n) .
On a limx→+∞ ƒ(x) = 0 donc limn→+∞ un = 0.