accueil / sommaire cours première S / introduction

Introduction

Exemple 1

Soit le polynôme P de degré 5 défini par : P(x) = 7x⁵ + 6x³ − 5x² + x − 9

Soit l'appplication a qui à chaque degré k inférieur ou égale à 5, associe le coefficient du monome de degré k dans P(x).

on a obtient :

a : 0 → a(0) = − 9

   : 0 → a(1) = 1

   : 0 → a(2) = − 5

   : 0 → a(3) = 6

   : 0 → a(4) = 0

   : 0 → a(5) = 7

La source de a est I = { 0, 1, 2, 3, 4, 5 } est une partie de l'ensembles des entiers naturels 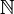que nous noterons dans la suite de ce cours N . Nous parlons d'une suite à termes réels défini sur la partie I de N.

Pour tout n élément de I de N, nous notons a(n) = a_n (se lit : a de n est egale a indice n) nous obtenons alors :

a₀ = − 9; a₁ = 1; a₂ = − 5; a₃ = − 6; a₄ = 0; a₅ = 7.

La suite a est notée (a_n)_n∈I suite de terme général a_n, avec n∈I.

Exemple 2

U est l'application de N* dans ℜ (l'ensemble des réels) qui a tout entier n ∈ N*, associe le nombre entier naturel impair (par ordre croissant).

N* partie de N, U est une suite à termes réels défine sur N*.

u(1) = 1 = 2 × 1 − 1

u(2) = 3 = 2 × 2 − 1

u(3) = 5 = 2 × 3 − 1

u(4) = 7 = 2 × 4 − 1

u(5) = 9 = 2 × 5 − 1

u(50) = 99 = 2 × 50 − 1

u(600) = 1199 = 2 × 600 − 1

Nous montrerions pour tout n ∈ N*, u(n) = 2n − 1 et en notation indicielle u(n) = u_n.

La suite U est notée (u_n)_n∈N* , suite de terme général u_n= 2n − 1.